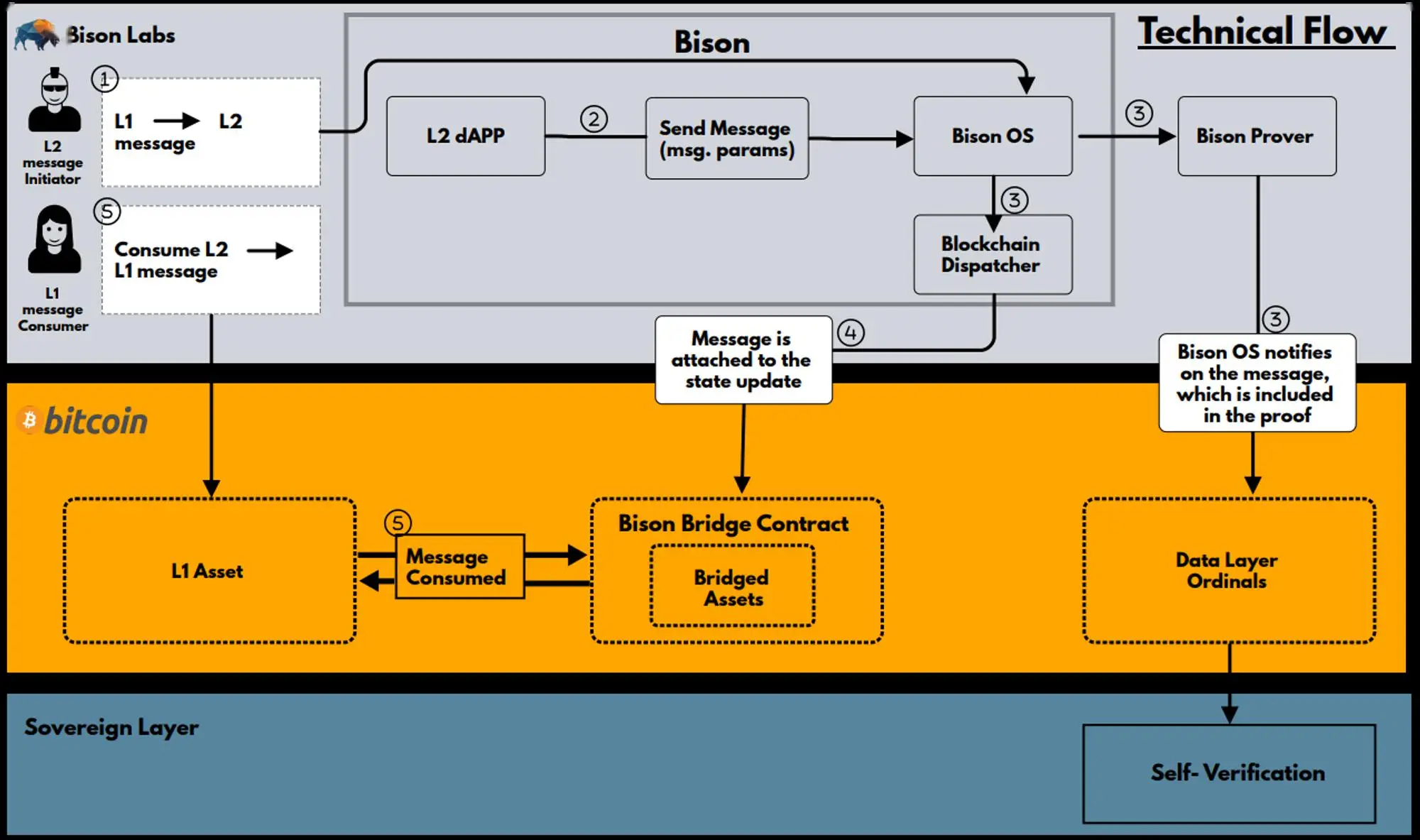
dijkstra算法是一种用于求解图中最短路径的经典算法。它以其高效性和准确性而闻名,被广泛应用于网络路由、地理信息系统等领域。在本文中,我将介绍dijkstra算法的原理和实现细节,并通过具体案例说明其工作过程。
- dijkstra算法是一种用于求解最短路径的图算法。
-它通过不断更新起始点到其他节点的距离值,逐步扩展最短路径集合,最终找到起始点到目标节点的最短路径。
- dijkstra算法采用贪心策略,每次选择距离起始点最近的节点进行扩展。
1.初始化:
首先,我们需要对图进行初始化。给定一个有向带权图G和一个起始节点s,我们将所有节点的距离值初始化为无穷大,起始节点s的距离值为0。
2.选择最近节点:

接下来,我们从未处理的节点中选择距离起始点s最近的节点v,并将其加入到最短路径集合中。此时,我们可以确定起始点s到节点v的最短路径。
3.更新距离值:
然后,我们遍历节点v的所有邻居节点,对于每个邻居节点u,我们计算起始点s经过节点v到达节点u的距离。如果这个距离小于节点u当前的距离值,我们就更新节点u的距离值。
whatsapp官方下载中文版:https://jrxxgk.com/sjyx/17869.html
